From Unsupervised CNN Deep Learning Classification to Vector Similarity Metrics
Pairwise vector similarity measures play significant roles in various data mining tasks. Finding matching pairs supports solving problems such classification, clustering or community detection and finding diversified pairs problems like outlier detection.One of the problems related to word pair dissimilarities is called in psychology 'free associations'. This is psychoanalysis method that is being used to get into unconscious process. In this study we will show how to find unexpected free associations by symmetry metrics.
We introduced a nontraditional vector similarity measure, symmetry metrics in our previous post "Symmetry Metrics for High Dimensional Vector Similarity". These metrics are based on transforming pairwise vectors to GAF images and classifying images through CNN image classifcation. In this post we will demonstrate how to use symmetry metrics to find dissimilar words pairs.
Introduction
Free Associations
Free Associations is a psychoanalytic technique that was developed by Sigmund Freud and still used by some therapists today. Patients relate to whatever thoughts come to mind in order for the therapist to learn more about how the patient thinks and feels. As Freud described it: "The importance of free association is that the patients spoke for themselves, rather than repeating the ideas of the analyst; they work through their own material, rather than parroting another's suggestions"
In our posts to detect semantically similar or dissimilar word pairs we experimented with data about Psychoanalysis taken from Wikipedia and used different techniques that all start with the following steps:
- Tokenize text file and removed stop words
- Transform words to embedded vectors through models like Word2Vec, Glove, BERT or other.
- Select pairs of words that stay next to each other in the document.
In our post "Word2Vec2Graph - Psychoanalysis Topics" we showed how to find free associations using Word2Vec2Graph techniques. For vector similarity measures we used cosine similarities. To create Word2Vec2Graph model we selected pairs of words located next to each other in the document and built a direct graph on word pairs with words as nodes, word pairs as edges and vector cosine similarities as edge weights. This method was publiched in 2021: "SEMANTICS GRAPH MINING FOR TOPIC DISCOVERY AND WORD ASSOCIATIONS"
In another post - "Free Associations" - we demonstrated a different method - word pair similarity based on unsupervised Convolutional Neural Network image classification. We joined word vector pairs reversing right vectors, tranformed joint vectors to GAF images and classified them as 'similar' and 'different'.
In this post we will show how to predict word similarity measures using a novel technique - symmetry metrics.
Symmetry Metrics
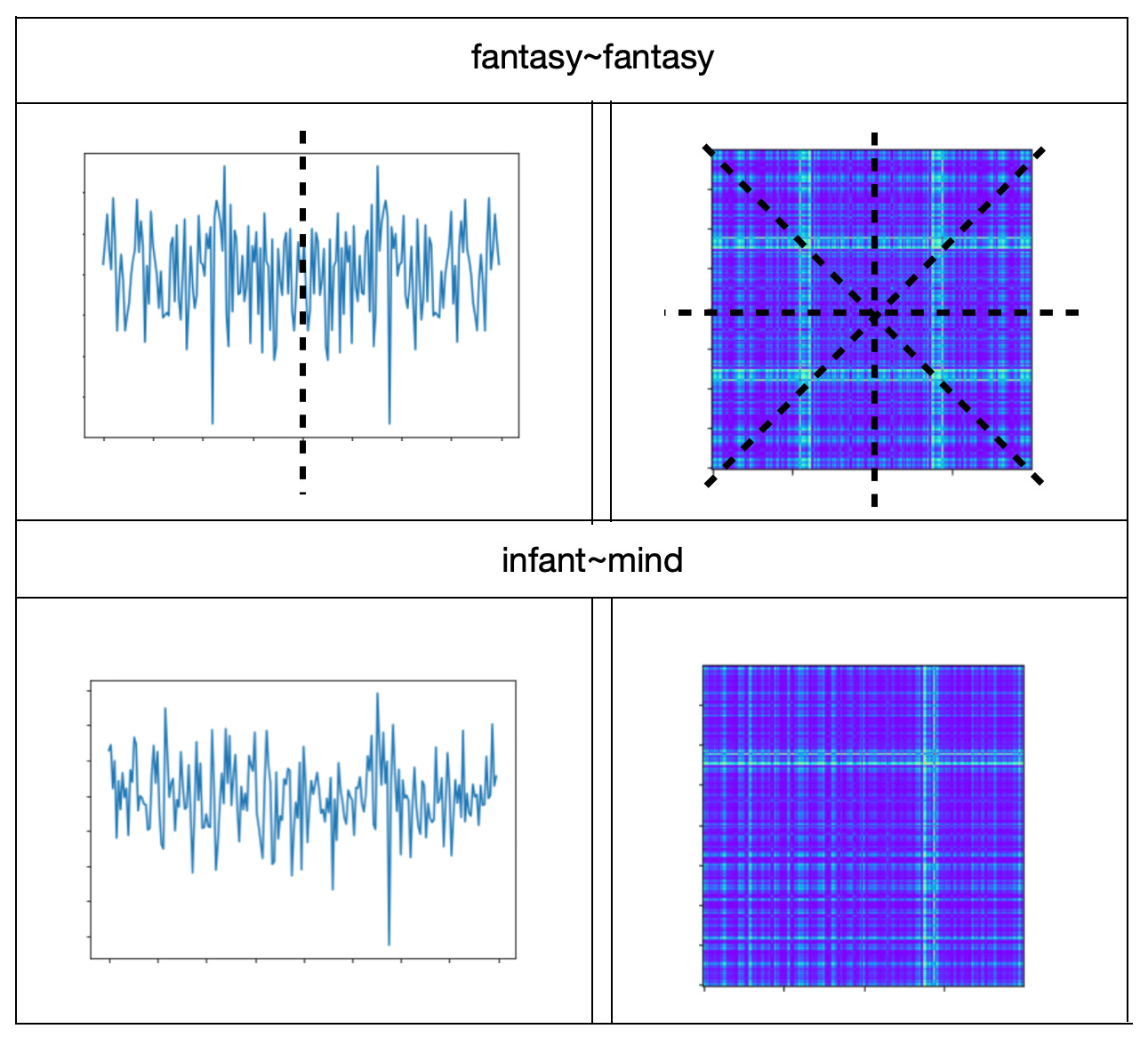
Vector similarity measures on large amounts of high-dimensional data has become essential in solving many machine learning problems such as classification, clustering or information retrieval. Vector similarity measures are being used for solving problems such as classification or clustering that usually looking for pairs that are closed to each other. In the previous post "Symmetry Metrics for High Dimensional Vector Similarity" we introduced symmetry metrics for high dimensional vector similarity. These metrics are based on unsupervised pairwise vector classification model - "Unsupervised Deep Learning for Climate Data Analysis" - that is implemented through transforming joint vectors to GAF images and classifying images as symmetric or asymmetric. Symmetry metric is defined as a probability of GAF image ran through trained model and get to the ’same’, i.e. 'symmetric' class.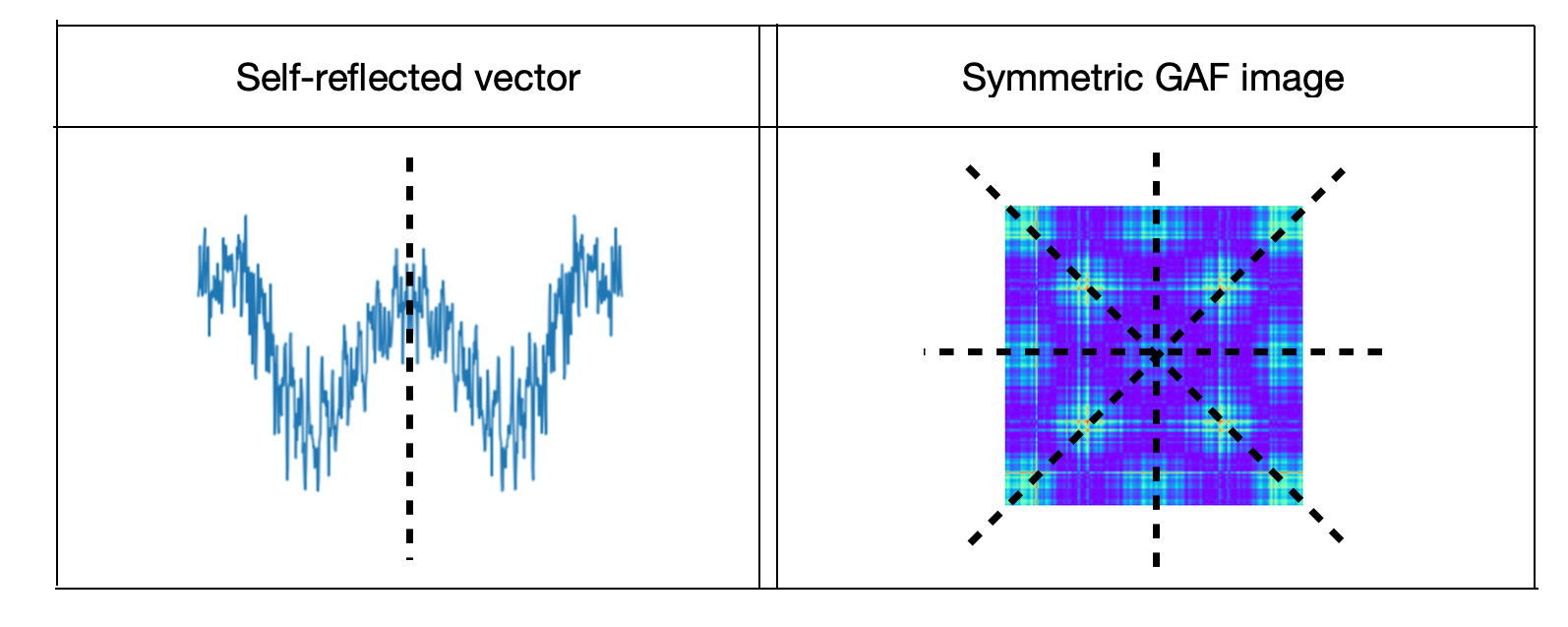
To distinguish between similar and dissimilar vector pairs this mode classifies data to 'same' and 'different' classes. Trained data for the 'same' class consists of self-reflected, mirror vectors and 'different' class of non-equal pairs. Visually mirror vectors are represented as symmetric images and 'different' pairwise vector as asymmetric images. Similarity metric is defined as a probability of pairwise vectors to get into the 'same' class.
In this post we will show how to apply trained unsupervised GAF image classification model to find vector similarities for entities taken from different domain. We will experiment with model trained on daily temperature time series data and apply it to word pair similarities.
Methods
Unsupervised Vector Classification Model
In one of our previous posts we introduced a novel unsupervised time series classification model. For this model we are embedding entities to vectors and combining entity pairs to pairwise vectors. Pairwise vectors are transformed to Gramian Angular Fields (GAF) images and GAF images are classified to symmetric or asymmetric classes using transfer learning CNN image classification. We examined how this model works for entity pairs with two-way and one-way relationships and indicated that it is not reliable for classification of entity pairs with two-way relationships.In this post we will use this method for one-way related pairs of words that are located next to each other in the document. We will generate pairwise word vectors for left and right words, transform joint vectors to GAF images and run these images through trained model to predict word similaritites through symmetry metrics.
Data Preparation
For data processing, model training and interpreting the results we will use the following steps:- Tokenize text and transform tokens to vectors
- Get pairs of co-located words and create joint vectors
- Transform joint vectors to GAF images
- Get similarity metrics based on interpretation of trained CNN image classification model
Transform Vectors to Images
As a method of vector to image translation we used Gramian Angular Field (GAF) - a polar coordinate transformation based techniques. We learned this technique in fast.ai 'Practical Deep Learning for Coders' class and fast.ai forum 'Time series/ sequential data' study group. This method is well described by Ignacio Oguiza in Fast.ai forum 'Time series classification: General Transfer Learning with Convolutional Neural Networks'.
To describe vector to GAF image translation Ignacio Oguiza referenced to paper Encoding Time Series as Images for Visual Inspection and Classification Using Tiled Convolutional Neural Networks.
Training of Unsupervised Vector Classification Model
For model training we used fast.ai CNN transfer learning image classification. To deal with comparatively small set of training data, instead of training the model from scratch, we followed ResNet-50 transfer learning: loaded the results of model trained on images from the ImageNet database and fine tuned it with data of interest. Python code for transforming vectors to GAF images and fine tuning ResNet-50 is described in fast.ai forum.
Use Results of Trained Models
To calculate how similar are vectors to each other we will combine them as joint vectors and transform to GAF images. Then we will run GAF images through trained image classification model and use probabilities of getting to the ’same’ class as symmetry metrics. To predict vector similarities based on the trained model, we will use fast.ai function 'learn.predict'.Experiments
Transform Text Data to Words
As a data source we will use data about Psychoanalysis taken from Wikipedia. First, we will tokenize text data and exclude stop words:modelWV = api.load("glove-wiki-gigaword-100")
tokenizer = RegexpTokenizer(r'\w+')
tokenizer =RegexpTokenizer(r'[A-Za-z]+')
tokens = tokenizer.tokenize(file_content)
STOPWORDS = set(stopwords.words('english'))
dfStopWords=pd.DataFrame (STOPWORDS, columns = ['words'])
dfTokens = pd.DataFrame (tokens, columns = ['token'])
dfTokens['token'] = dfTokens['token'].str.lower()
dfTokens['len']=dfTokens['token'].str.len()
dfTokens=dfTokens[dfTokens['len']>3]
dfTokens=dfTokens.replace({'token': {'/': ' '}}, regex=True)
df_excluded = dfTokens[~dfTokens['token'].isin(dfStopWords['words'].values)].reset_index(drop=True)
tokenz = df_excluded.filter(['token'], axis=1)
Transform Words to Vectors
Next, we will transform words to vectors through Glove model:modelWV = api.load("glove-wiki-gigaword-100")
token=tokenz['token'].values.tolist()
listWords=[]
listVectors=[]
for word in token:
try:
listVectors.append(modelWV[word])
listWords.append(word)
except KeyError:
x=0
dfWords=pd.DataFrame(listWords,columns=['word'])
dfVectors=pd.DataFrame(listVectors)
dfWordVec=pd.concat([dfWords,dfVectors],axis=1)Create Pairwise Vectors
In our previous posts we described the process of data preparation for pairwise vector method, model training and interpretation techniques are described in details in another post of our technical blog. In this post we followed the steps:- Create Left vectors with column 'word1' and Right vectors with column 'word2'
- Delete the first row from Right vectors and reverse them
- Delete the last row from Left vectors
- Concatenate Left and Right vectors
- Concatenate word1 and word2 to column pair as 'word1'~'word2'
- Drop duplicates
- Split to metadata [word1,word2,pair] and numeric arrays
dfWordVec1=dfWordVec.rename({'word':'word1'}, axis=1)
dfWordVec2=dfWordVec.rename({'word':'word2'}, axis=1)
leftVecWV=dfWordVec1.iloc[:-1,:]
leftVecWV.reset_index(inplace=True, drop=True)
rightVecWV=dfWordVec2[dfWordVec2.columns[::-1]].reset_index(drop=True)
rightVecWV = rightVecWV.iloc[1: , :].reset_index(drop=True)
pairVecWV0=pd.concat([leftVecWV, rightVecWV], axis=1)
pairVecWV0['pair'] = pairVecWV0['word1'].astype(str) + '~' + pairVecWV0['word2'].astype(str)
pairVecWV=pairVecWV0.drop_duplicates()
pairVecWV=pairVecWV.reset_index(drop=True)
pairMetadata= pairVecWV[['word1','word2','pair']]
pairVecWVvalues=pairVecWV
pairVecWVvalues.drop(['word1','word2','pair'], axis=1, inplace=True)
fXpairWV=pairVecWVvalues.fillna(0).values.astype(float)Transform Vectors to Images
As a method of vector to image translation we used Gramian Angular Field (GAF) - a polar coordinate transformation based techniques. We learned this technique in fast.ai 'Practical Deep Learning for Coders' class and fast.ai forum 'Time series/ sequential data' study group.
import matplotlib.pyplot as plt
plt.figure(figsize=(8, 8))
from pyts.image import GramianAngularField as GASF
image_size = 200
gasf = GASF(image_size)
fXpair_gasfWV = gasf.fit_transform(fXpairWV)
plt.plot(fXpairWV[2073])
plt.imshow(fXpair_gasfWV[2073], cmap='rainbow', origin='lower')
Train the Model
Time series classification model training was done on fast.ai transfer learning method. This model is described in detail in "Unsupervised Deep Learning for Climate Data Analysis" post. Model was trained on data about daily temperature for 1980 to 2020 years from 1000 most populous cities in the world. The training model accuracy metric was about 96.5 percent.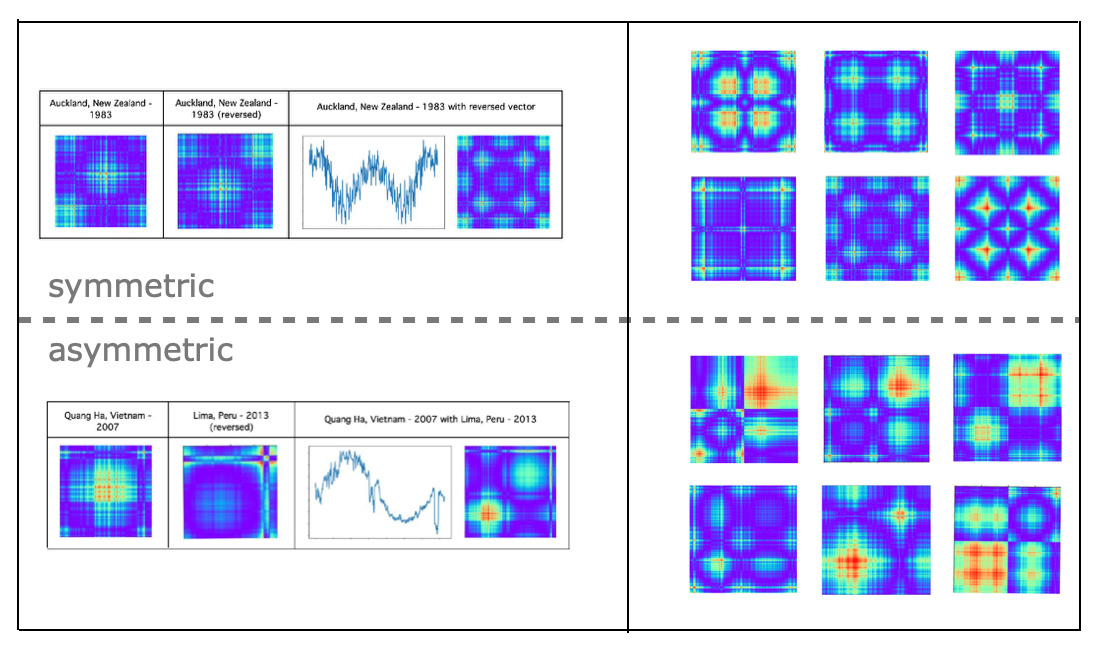
Symmetry Metrics based on Results of Trained Models
To calculate symmetry metrics we will create pairwise vectors by concatenating word vector pairs. Then we ran GAF images through the trained image classification model and used probabilities of getting to the ’same’ class as symmetry metrics. To predict vector similarities based on the trained model, we used fast.ai function 'learn.predict':PATH_IMG='/content/drive/My Drive/city2/img4'
data = ImageDataBunch.from_folder(PATH_IMG, train=".", valid_pct=0.23,size=200)
learn = learner.cnn_learner(data2, models.resnet34, metrics=error_rate)
learn.load('stage-1a')Symmetry Metrics on Pairs of Words
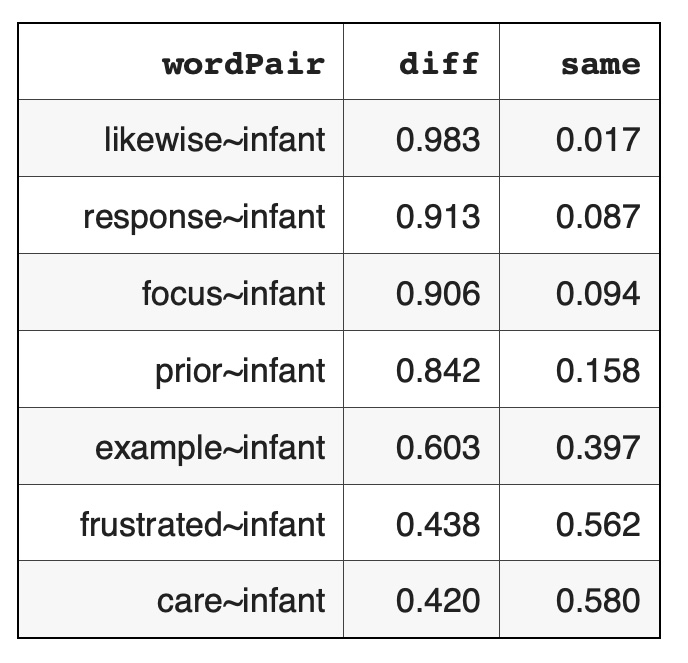
We calculated symmetry metrics on pairs of co-located words or 2-grams from Psychoanalysis Wikipedia data. The distribution of statistics on word pair similarities shows that there are much less dissimilar word pairs that similar word pairs: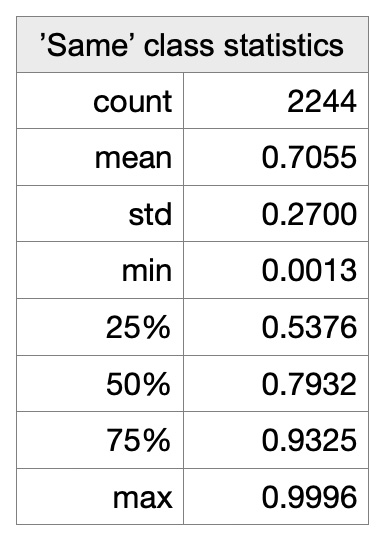
Here are some word pair examples of dissimilar and similar neighbors for the word 'infant' - {infant - word} pairs
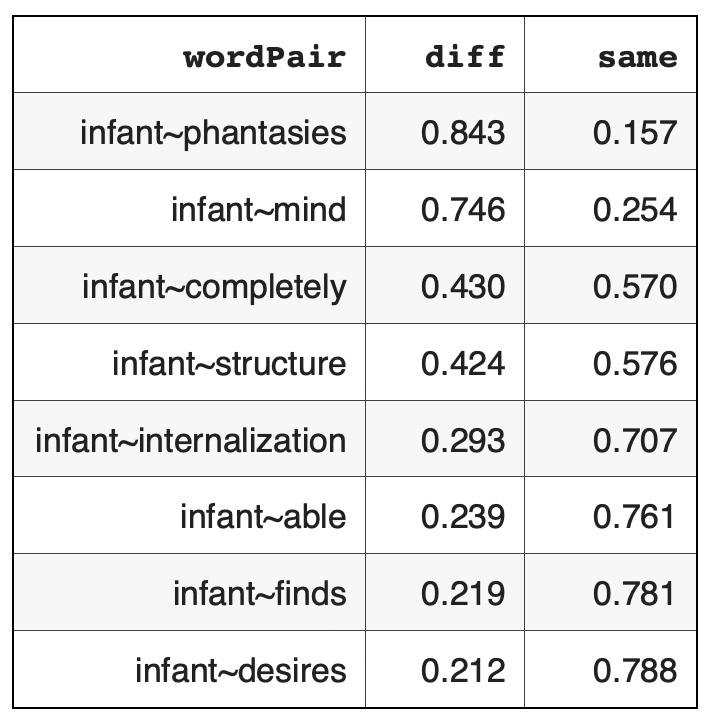Here are word pairs taken in opposite direction: {word - infant} pairs:
